小學生數學典故:奇妙的分形世界
來源:濟南奧數網整理 文章作者:奧數網編輯 2011-12-06 17:31:27

生活中出處充滿數學的趣味,在這里濟南奧數網小編為大家整理了一些小學生數學故事,希望濟南的家長和孩子能在快樂中了解數學,愛上數學。
小學生數學典故:奇妙的分形世界
如果讓你考慮一個這樣的問題:“具有有限面積的平面圖形,其周長是有限的,還是無限的呢?”你會毫不猶豫地說:“當然周長也是有限的。”
在我們現在學習的幾何中,人們總是用諸如點、線、平面、三角形、正方形、圓這樣的對象和概念來描述我們生存的這個世界。然而1906年瑞典數學家科克作了一條“雪花曲線”,它的面積是有限的,然而它的周長是無限的。
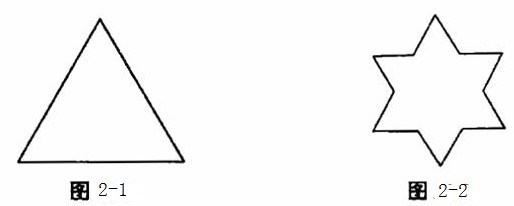
雪花曲線的具體做法是這樣的。先作一個等邊三角形(如圖2-1),再把每邊三等分,將居中的1/3部分向外作一個小等邊三角形,并把每一個小等邊三角形的底抹掉,得到一個六角星形(如圖2-2));再在六角星形的每一條邊上以同樣的方法向外作出更小的等邊三角形,于是曲線變得越來越長,開始像一片雪花了(如圖2-3))。再如此作下去,曲線將變得越來越長,圖形也更美麗(如圖2-4)。如果不斷地作下去,則曲線可以要多長有多長,若無限地如此作下去,自然就有無限周長了。而這個圖形的面積,通過計算,最多只能是原來三角形的8/5倍。

意大利數學家歐內斯托·切薩羅曾對科克雪花曲線作過如下描述:這個曲線最使我們注意的地方是任何部分都與整體相似。這個結構的每一個小三角形包含著一個適當比例縮小的整體形狀。這個形狀包含著每一小三角形的縮小形式,后者又包含縮得更小的整體形狀,如此下去以致無窮。就是這個在它所有的無論怎樣小的部分都保持著相似的性質,使這曲線看上去是如此的奇妙。要是它在現實中出現,那就必須把它完全除去才能摧毀它。否則的話,它將會從它的三角形的深處重新不停地生長起來,就像宇宙本身一樣。
相關文章
- 小學1-6年級作文素材大全
- 全國小學升初中語數英三科試題匯總
- 小學1-6年級數學天天練
- 小學1-6年級奧數類型例題講解整理匯總
- 小學1-6年級奧數練習題整理匯總
- 小學1-6年級奧數知識點匯總
- 小學1-6年級語數英教案匯總
- 小學語數英試題資料大全
- 小學1-6年級語數英期末試題整理匯總
- 小學1-6年級語數英期中試題整理匯總
- 小學1-6年語數英單元試題整理匯總





