·每道題的答題時間不應(yīng)超過15分鐘。答案明日公布！

　　難度：★★★★

　　小學(xué)四年級奧數(shù)天天練：證明題

　　從2、4、6、…、30這15個偶數(shù)中，任取9個數(shù)，證明其中一定有兩個數(shù)之和是34。
 

　　【答案】

　　我們用題目中的15個偶數(shù)制造8個抽屜：

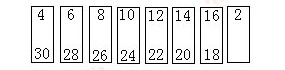
　　凡是抽屜中有兩個數(shù)的，都具有一個共同的特點：這兩個數(shù)的和是34。
　　現(xiàn)從題目中的15個偶數(shù)中任取9個數(shù)，由抽屜原理（因為抽屜只有8個），必有兩個數(shù)在同一個抽屜中.由制造的抽屜的特點，這兩個數(shù)的和是34。



　　難度：★★★★★

　　小學(xué)四年級奧數(shù)天天練：邏輯推理

　　六年級有100名學(xué)生，他們都訂閱甲、乙、丙三種雜志中的一種、二種或三種。問：至少有多少名學(xué)生訂閱的雜志種類相同？

　　【答案】

　　首先應(yīng)當(dāng)弄清訂閱雜志的種類共有多少種不同的情況。

　　訂一種雜志有：訂甲、訂乙、訂丙3種情況；

　　訂二種雜志有：訂甲乙、訂乙丙、訂丙甲3種情況；

　　訂三種雜志有：訂甲乙丙1種情況。

　　總共有3＋3＋1=7（種）訂閱方法。我們將這7種訂法看成是7個"抽屜"，把100名學(xué)生看作100件物品。因為100＝14×7＋2。根據(jù)抽屜原理2，至少有14＋1＝15（人）所訂閱的報刊種類是相同的。